近日，华中科技大学物理学院祝雪丰教授团队在Stiefel-Whitney类的声学高阶拓扑半金属实验观测方面取得进展，相关工作以「Demonstration of acoustic higher-ordertopological Stiefel-Whitney semimetal」为题发表在《物理评论快报》（Physical Review Letter）上。
该工作的理论方面得到了中南大学倪祥教授的详细指导，武汉大学余睿教授和华中科技大学郇真教授也提供很多宝贵的建议。物理学院博士生向霄为论文的第一作者，祝雪丰教授、彭玉桂副教授及中南大学的倪祥教授为论文的共同通讯作者。华中科技大学物理学院博士生高峰、科研助理武朋，香港科技大学（广州）吴肖肖助理教授及南京大学陈召宪博士后对该工作也有重要贡献。华中科技大学为该工作的第一完成单位。
到目前为止，数学上有四种不同类型的示性类：Chern类、SW类、Pontryagin类和Euler类。过去十年以来，Chern类拓扑绝缘体及其拓扑不变量，如陈数、自旋陈数、镜像陈数、Fu-Kane不变量等已广泛应用于凝聚态拓扑相位，欧拉类近几年也逐渐被研究人员所关注和探索，但也意味着其他示性类在凝聚态物理中尚未被很好的理解和运用。SW示性类在数学领域有着广泛的影响。 然而，迄今为止，在经典波物理学和凝聚态物理学中，SW类的实验研究很少。利用投影对称性相关数学，科研人员近期提出了高阶拓扑Stiefel-Whiney半金属(HOTSWS)的理论模型。然而，HOTSWS相关实验在经典波体系少有报导。
在本工作中，研究团队通过使用投影对称性相关的规范场来实现声学 HOTSWS，它对应一个三维结构中的节线环半金属。声学HOTSWS的核心特征是拓扑态同时受到两个不同阶的SW拓扑荷（即w₁和w₂）保护，表面态和铰链态理论上出现一个频率处；在PT对称性下HOTSWS的本征态可以对应实的向量丛，这与由复向量丛刻画的陈类拓扑态有本质的区别。通过本征声压分布分析，研究团队定量计算了声学系统中的这些拓扑不变量。在w₁和w₂中，二阶拓扑不变量w₂由HOTSWS的节点环携带，这类节点环极其稳定，在对称保护的参数变换下，能带可能翻转但节线环不会消失。
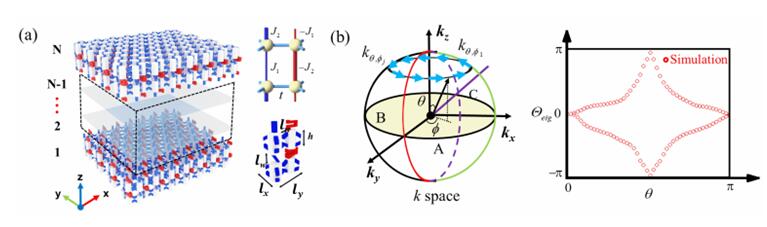
图1 声学HOTSWS的模型示意图和SW不变量的计算
图1展示了研究团队HOTSWS的声学模型。声学结构由六边形声学谐振器和耦合管组成的声子晶体，其中蓝色和红色耦合管分别表示正耦合和负耦合。研究团队通过Wilson loop的方法去计算二阶SW不变量：在第一BZ的k点处定义一个球体，其包裹着一个节点环。蓝色箭头（N波矢量）在k空间中以固定的方位角标记圆环，右图的Wilson loop谱表明w₂= 1.
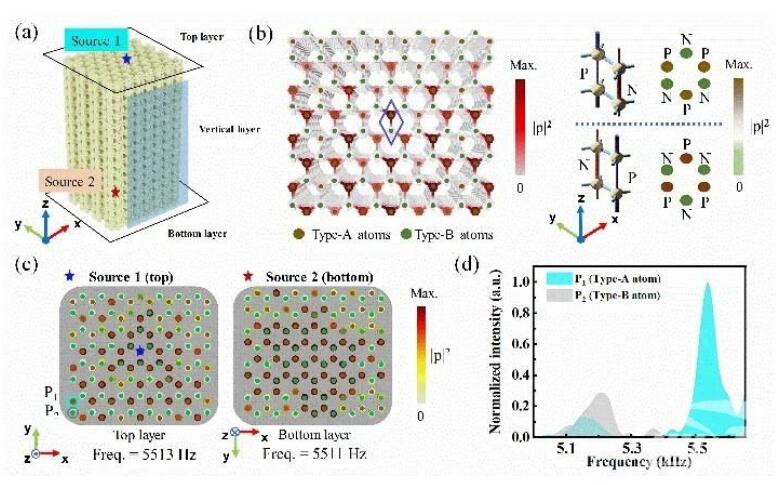
图2 实验观测的表面模态
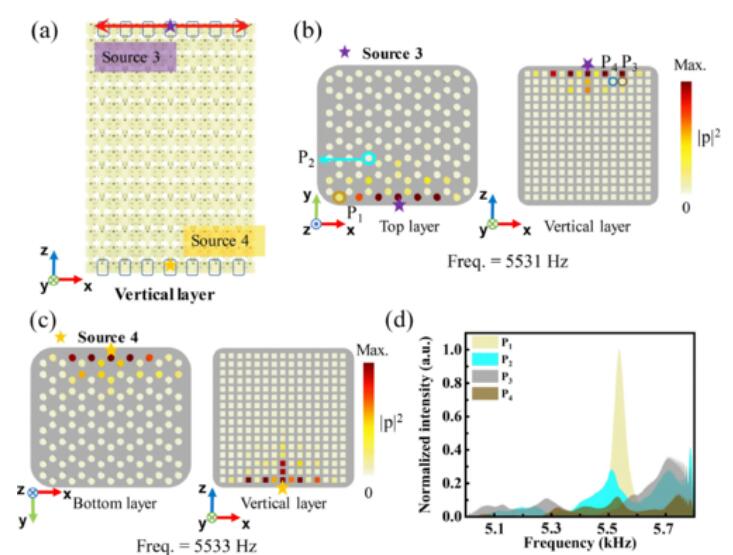
图3 实验观测的铰链模态
研究团队进一步通过实验观察到拓扑铰链态和表面态在同一频率处共存。表面和铰链态被证明分别选择性地分布在声子晶体特定的表面和边缘上，如图2和图3所示。研究团队的工作表明，HOTSWS 是 PT 对称系统中一种新颖的高阶拓扑相，并为研究 SW 类拓扑相提供了一个理想平台。
该研究获得了国家自然学科基金的资助。
论文链接：
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.197202
来源：华中科技大学，爱科会易仅用于学术交流。
近日，华中科技大学物理学院祝雪丰教授团队在Stiefel-Whitney类的声学高阶拓扑半金属实验观测方面取得进展，相关工作以「Demonstration of acoustic higher-ordertopological Stiefel-Whitney semimetal」为题发表在《物理评论快报》（Physical Review Letter）上。
该工作的理论方面得到了中南大学倪祥教授的详细指导，武汉大学余睿教授和华中科技大学郇真教授也提供很多宝贵的建议。物理学院博士生向霄为论文的第一作者，祝雪丰教授、彭玉桂副教授及中南大学的倪祥教授为论文的共同通讯作者。华中科技大学物理学院博士生高峰、科研助理武朋，香港科技大学（广州）吴肖肖助理教授及南京大学陈召宪博士后对该工作也有重要贡献。华中科技大学为该工作的第一完成单位。
到目前为止，数学上有四种不同类型的示性类：Chern类、SW类、Pontryagin类和Euler类。过去十年以来，Chern类拓扑绝缘体及其拓扑不变量，如陈数、自旋陈数、镜像陈数、Fu-Kane不变量等已广泛应用于凝聚态拓扑相位，欧拉类近几年也逐渐被研究人员所关注和探索，但也意味着其他示性类在凝聚态物理中尚未被很好的理解和运用。SW示性类在数学领域有着广泛的影响。 然而，迄今为止，在经典波物理学和凝聚态物理学中，SW类的实验研究很少。利用投影对称性相关数学，科研人员近期提出了高阶拓扑Stiefel-Whiney半金属(HOTSWS)的理论模型。然而，HOTSWS相关实验在经典波体系少有报导。
在本工作中，研究团队通过使用投影对称性相关的规范场来实现声学 HOTSWS，它对应一个三维结构中的节线环半金属。声学HOTSWS的核心特征是拓扑态同时受到两个不同阶的SW拓扑荷（即w₁和w₂）保护，表面态和铰链态理论上出现一个频率处；在PT对称性下HOTSWS的本征态可以对应实的向量丛，这与由复向量丛刻画的陈类拓扑态有本质的区别。通过本征声压分布分析，研究团队定量计算了声学系统中的这些拓扑不变量。在w₁和w₂中，二阶拓扑不变量w₂由HOTSWS的节点环携带，这类节点环极其稳定，在对称保护的参数变换下，能带可能翻转但节线环不会消失。
图1 声学HOTSWS的模型示意图和SW不变量的计算
图1展示了研究团队HOTSWS的声学模型。声学结构由六边形声学谐振器和耦合管组成的声子晶体，其中蓝色和红色耦合管分别表示正耦合和负耦合。研究团队通过Wilson loop的方法去计算二阶SW不变量：在第一BZ的k点处定义一个球体，其包裹着一个节点环。蓝色箭头（N波矢量）在k空间中以固定的方位角标记圆环，右图的Wilson loop谱表明w₂= 1.
图2 实验观测的表面模态
图3 实验观测的铰链模态
研究团队进一步通过实验观察到拓扑铰链态和表面态在同一频率处共存。表面和铰链态被证明分别选择性地分布在声子晶体特定的表面和边缘上，如图2和图3所示。研究团队的工作表明，HOTSWS 是 PT 对称系统中一种新颖的高阶拓扑相，并为研究 SW 类拓扑相提供了一个理想平台。
该研究获得了国家自然学科基金的资助。
论文链接：
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.197202
来源：华中科技大学，爱科会易仅用于学术交流。
