- 国内站
- 国际站
No data


2024年7月10日,中国科学技术大学潘建伟、陈宇翱及姚星灿共同通讯,在Nature 在线发表题为「Antiferromagnetic phase transition in a 3D fermionic Hubbard model」的研究论文。该研究报告了一个由锂-6原子组成的三维费米子Hubbard系统的反铁磁相变的观察,该系统在一个均匀的光学晶格中有大约80万个位点。据悉,这是潘建伟院士团队2024年在Nature/Science发表的第4篇研究论文。据不完全统计,自潘建伟教授在中科大建立课题组以来,他已发表了13篇Science和18篇Nature。以下为最新论文导读,文末附有潘建伟院士团队2024年在Nature/发布的其余3篇论文链接,以飨读者。
本研究中,中国科学技术大学潘建伟院士、陈宇翱教授和姚星灿教授报告了在三维费米子哈伯德系统中观察到的反铁磁相变,该系统由均匀光学晶格中的锂-6 原子组成,具有大约 800,000 个位点。当相互作用强度、温度和掺杂浓度被微调到接近它们各自的临界值时,观察到自旋结构因子急剧增加。这些观察结果可以通过幂律散度来很好地描述,海森堡普适性类别的临界指数为 1.396。在半填充和最佳相互作用强度下,测得的自旋结构因子达到123(8),表明反铁磁相的建立。此结果为探索 FHM 的低温相图提供了机会。相关成果以「Antiferromagnetic phase transition in a 3D fermionic Hubbard model」为题发表在Nature上,第一作者为Hou-Ji Shao, Yu-Xuan Wang为共同一作。

论文截图

潘建伟,1970年3月生于浙江东阳,实验物理学博士,中国科学技术大学教授,中国科学院院士,发展中国家科学院院士,奥地利科学院外籍院士,现任中科院量子信息与量子科技创新研究院院长。2001年,潘建伟在奥地利维也纳大学完成五年的博士后研究后,回到母校中国科学技术大学,成为近代物理系的教授,当时他年仅31岁。回国后,他带领团队专注于量子光学、量子信息和量子力学基础问题的研究,推动了中国量子信息技术的进程,成为国际上颇具影响力的科学家,被誉为「最接近诺贝尔奖的中国科学家」。
三维费米子哈伯德模型中的反铁磁相变
费米子哈伯德模型(FHM)描述了由强电子-电子相关性引起的广泛的物理现象,包括非常规超导的推测机制。然而,解决其低温物理问题在理论上或数值上都具有挑战性。光学晶格中的超冷费米子提供了一个干净且控制良好的平台,为模拟FHM提供了一条途径。在半填充状态下掺杂FHM模拟器的反铁磁基态有望产生各种奇异相,为研究高温超导性提供有价值的见解。虽然在短距离和长距离上已经观察到反铁磁相关,但反铁磁相还没有实现,因为它需要在一个大而均匀的量子模拟器中足够低的温度。
费米子哈伯德模型(FHM)的哈密顿量采用一种简单的形式,由两项组成:一项表示最近邻居的跳跃t,另一项表示具有相反自旋的电子之间的现场相互作用U。FHM可以描述广泛的强相关电子物理,包括相互作用驱动的金属到绝缘体的转变,量子磁性和非常规超导性。然而,尽管经过了60年的深入研究,对其低温物理特性的准确理解仍然未知。精确的解析解只能在一维或无限空间维度的极限中得到。尽管已经开发了各种先进的数值技术,但控制的定量研究仍然很少,特别是在低温状态下。量子蒙特卡罗(QMC)模拟通常会遇到负号问题,而其他方法,如密度矩阵重整化组,由于计算机内存需求随着系统大小呈指数增长而受到限制。即使在半填充的情况下,对于低温下足够大的系统,模拟在计算上也会变得令人望而却步。
在过去的二十年中,现代激光和原子技术的发展导致了在光学晶格中使用超冷原子的FHM的实验实现。对哈密顿参数的精确控制使这些超冷原子系统成为探索低温和掺杂状态下FHM强相关特性的强大平台,这些特性是通过分析和数值方法难以获得的。要实现这一目标,关键和不可避免的一步是在FHM中实现Néel相变和反铁磁相。这需要达到低温,制备大型均匀系统和开发新的探测技术。沿着这些思路,已经取得了许多重要进展。在三维空间中,莫特相和带绝缘相的实现,以及短程量子磁性的观察已被报道。值得注意的是,自旋结构因子(SSF)在比nsamel温度TN高约40%的温度下达到了Sπ≈2,表明存在短程反铁磁相关。
在这项工作中,研究人员开发了一个大型量子模拟器,通过结合两个关键进展来探索FHM的低温物理:在盒阱中产生低温均匀费米气体和展示具有均匀位势的三维(3D)平顶光学晶格。在半填充时,FHM的哈密顿量表现出SU(2)对称性,并且随着温度T的降低,它在TN处经历向反铁磁Néel相的转变,SU(2)对称性自发破坏。因此,该反铁磁相变与三维经典Heisenberg模型具有相同的普遍性,这意味着SSF应表现出发散性行为,其临界指数为γ≠(T−TN)−γ,且临界点指数为γ≃1.396。
实验方案和设置
为了研究3D费米哈伯德模型(FHM)中的量子磁性,作者结合盒式陷阱和平顶光学晶格的方法(图1),在中心区域直径49.5 μm内,确保最近邻跳跃t、现场相互作用U和化学势µ基本恒定。这种系统通过低温均质费米气体和近绝热晶格加载,有效实现低单粒子熵,进而制备具有极低3D费米子哈伯德系统单粒子熵的均匀费米气体。系统由6Li原子组成,分布在超精细能级|1⟩和|3⟩之间,且在568G磁场下被限制在圆柱形盒式阱内,达到密度约6.64×10¹²cm⁻³和0.041(1)TF的低温。在18ms内逐渐增加晶格深度并在12ms内调整磁场,实现不同现场相互作用U,最终生成t/h=1.40(1)kHz和U/h范围从6.04(2)kHz到28.83(9)kHz。图1b显示了U/t=11且半填充状态下的代表性原位图像,中心区域原子密度高度均匀。为研究系统内长程反铁磁序,使用了自旋敏感相干布拉格散射技术,图1d显示布拉格信号强度约为参考信号的100倍。
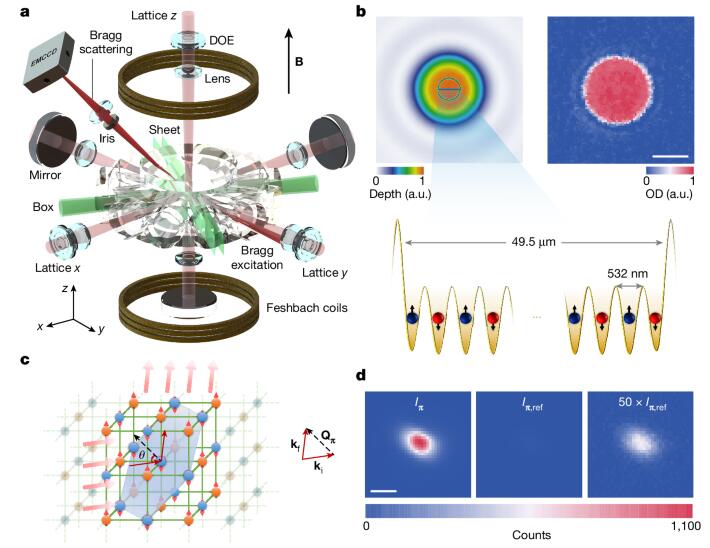
图 1|实验方案和设置
作者从半填充的费米哈伯德模型开始,研究其反铁磁相变(图2a)。在高温下,系统表现出金属行为(小U)或莫特绝缘态(大U),在TN以下和小U处,由自旋密度波(SDW)引起的尼尔跃迁,TN达到最大值时的最佳相互作用强度为Uopt。实验结果显示,在U ≈ 11.5t时,TN达到最大值,这是由于边界附近原子密度偏离半填充以及晶格势中残留无序性引起的。SSF的测量结果(图2b)显示,随着U的增加,Sπ从小值逐渐增加,在U ≈ 11.96t时达到最大,然后在U ≈ 20.62t时降至最低。作者发现,U/t ≤ 8和U/t ≥ 16的数据可以被Néel转变点捕捉,显示出系统在相互作用、温度和原子密度参数空间中接近临界点时的普遍性。
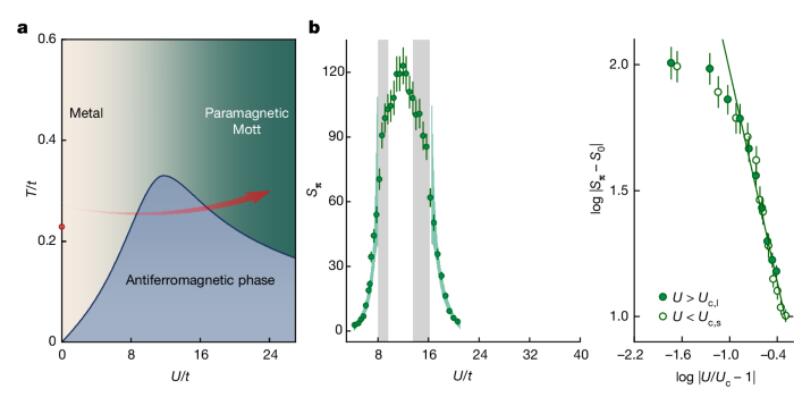
图 2|自旋结构因子 Sπ 作为 U/t 的函数
研究测量了Sπ作为每个粒子初始熵s的函数,并在图3a-d中显示了U/t≈11.75、8.21、18.06和5.31的结果。对于U≈11.75t和8.21t,幂律拟合显示临界熵分别为sc≈0.27kB和0.20kB(图3a、b)。相比之下,对于U≈18.06t,临界标度较弱,表明系统接近但未达到尼尔跃迁;对于U≈5.31t,临界缩放几乎不可辨别(图3c、d)。基于盒式阱和高温QMC数据的LDA计算,Sπ值与实验值吻合良好(U≈5.31t),但对于U≈8.21t,数值结果大于实验值,主要因非绝热性和晶格势中无序性。作者建议通过实验和数值比较确定温度。然而,由于误差较大和对s变化不敏感,使用图3中的s展示尼尔转变最为合适。考虑掺杂效应,理论预测掺杂10-20%时尼尔温度降低至零,且基态可能从反铁磁转变为不相称的SDW态,具体机制仍需进一步研究。
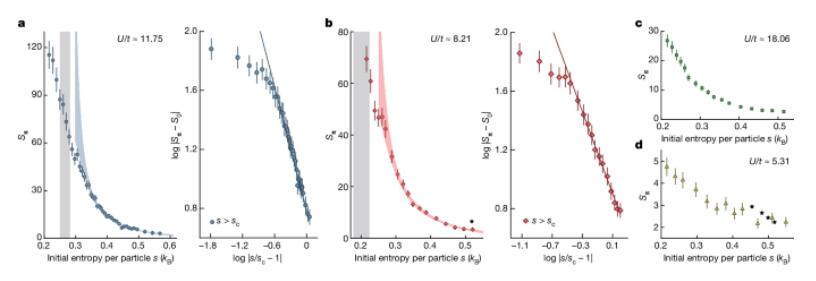
图 3:自旋结构因子 Sπ作为每个粒子 s 初始熵的函数
在实验中,作者在U ≈ 11.75t和半填充时,在最低温度下制备了费米子哈伯德系统。相图(图4a)显示纵轴表示费米子哈伯德系统每个粒子的熵sL,蓝点和粗箭头分别表示测量的s和估计的sL,作为每个晶格位点n的平均密度的函数,其中n = 1对应半填充。sL和s之间的差异表明熵的非绝热增加。Sπ的实验结果(图4b左)显示其在临界点附近急剧变化,实验数据在n < 0.91或n > 1.11时拟合良好,得到nc,s = 0.95(1)和nc,l = 1.07(1)的临界值。此外,双对数图(图4右)中,数据点折叠成斜率为-1.396的实线,表明与3D海森堡普适性一致,尽管实验数据不足以精确确定磁临界指数γ。
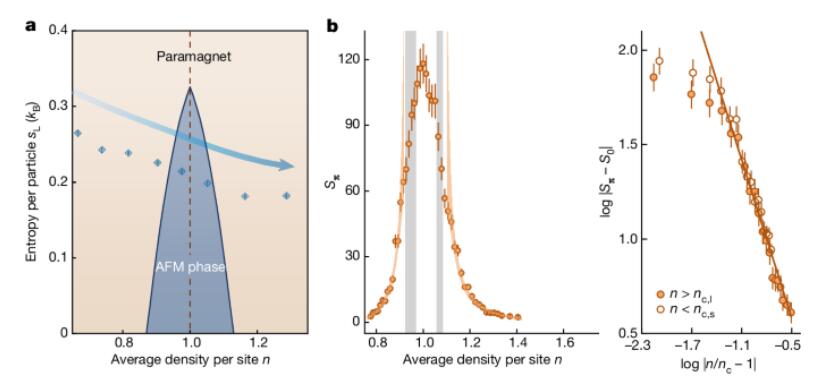
图 4|自旋结构因子 Sπ 作为每个位点平均密度 n 的函数
作者开发了一个先进的量子模拟平台,拥有约800,000个晶格位点,具有几乎均匀的哈伯德参数和远低于TN的温度,并观察到了SSF的关键分歧,为反铁磁相变提供了确凿证据。该装置为探索低温和掺杂的FHM25物理提供了机会,使作者能够通过调整层间耦合强度来研究3D或准2D中的奇异量子相,如更高维度的自旋电荷分离、排斥设置中的赝能隙和特定填充下的条纹顺序。这些研究可以通过自旋敏感布拉格光衍射、动量分辨微波光谱和长波长限制中的布拉格散射等技术实现。此外,通过在装置中添加光学超晶格,作者可以实现耦合平板阵列并探索可能的d波配对。这些量子模拟将提供有价值的实验数据,增强作者对量子磁性在高温超导机制中作用的理解。作者还计划通过调整原子相互作用以使其具有吸引力,在有吸引力的FHM中实现长期寻求的单带超流体,并在晶格背景下探索BCS-BEC交叉的基础物理现象。
该工作推进了对费米子哈伯德模型的理解,为进一步求解该模型、获取其低温相图奠定了基础,也首次展现了量子模拟在解决经典计算机无法胜任的重要科学问题上的巨大优势。相关成果以「Antiferromagnetic phase transition in a 3D fermionic Hubbard model」为题发表在Nature上,第一作者为Hou-Ji Shao, Yu-Xuan Wang为共同一作。
另外,2024年2月7日,中国科学技术大学潘建伟、姚星灿及陈宇翱共同通讯在Nature 在线发表题为「Observation and quantification of the pseudogap in unitary Fermi gases」的研究论文,该研究报告了通过动量分辨微波光谱精确测量费米子谱函数,在没有末态相互作用的虚假影响的情况下,在锂-6原子的均匀统一费米气体中观察到对波动驱动的赝隙。通过光谱分析,定量地确定了对间隙、逆对寿命和单粒子散射率的温度依赖性。该研究发现在超流体转变温度以上存在较大的赝隙。逆偶寿命表现为热激活指数行为,揭示了微观虚偶断裂和复合机制。得到的与温度无关的大单粒子散射率与普朗克极限所设定的散射率相当。总之,该研究的发现定量地描述了强相互作用费米气体中的赝隙,并支持了预形成对作为超流动性前兆的作用。(阅读原文:https://www.nature.com/articles/s41586-023-06964-y)
2024年5月2日,中国科学技术大学潘建伟及陆朝阳共同通讯在Science 在线发表题为「Realization of fractional quantum Hall state with interacting photons」的研究论文,该研究在二维电路量子电动力学系统上使用基于光子封锁和工程规范场的可编程片上平台演示了光子FQH态的晶格版本。(阅读原文:https://www.science.org/doi/10.1126/science.ado3912)
2024年5月15日,中国科学技术大学潘建伟及包小辉共同通讯在Nature 在线发表题为「Creation of memory–memory entanglement in a metropolitan quantum network」的研究论文,该研究报告了在城域上的多节点量子网络中创建内存-内存纠缠。(阅读原文:https://www.nature.com/articles/s41586-024-07308-0)
本篇论文链接:
https://www.nature.com/articles/s41586-024-07689-2
来源:高分子科学前沿,iNature,版权属于原作者,爱科会易仅用于学术交流
2024年7月10日,中国科学技术大学潘建伟、陈宇翱及姚星灿共同通讯,在Nature 在线发表题为「Antiferromagnetic phase transition in a 3D fermionic Hubbard model」的研究论文。该研究报告了一个由锂-6原子组成的三维费米子Hubbard系统的反铁磁相变的观察,该系统在一个均匀的光学晶格中有大约80万个位点。据悉,这是潘建伟院士团队2024年在Nature/Science发表的第4篇研究论文。据不完全统计,自潘建伟教授在中科大建立课题组以来,他已发表了13篇Science和18篇Nature。以下为最新论文导读,文末附有潘建伟院士团队2024年在Nature/发布的其余3篇论文链接,以飨读者。
本研究中,中国科学技术大学潘建伟院士、陈宇翱教授和姚星灿教授报告了在三维费米子哈伯德系统中观察到的反铁磁相变,该系统由均匀光学晶格中的锂-6 原子组成,具有大约 800,000 个位点。当相互作用强度、温度和掺杂浓度被微调到接近它们各自的临界值时,观察到自旋结构因子急剧增加。这些观察结果可以通过幂律散度来很好地描述,海森堡普适性类别的临界指数为 1.396。在半填充和最佳相互作用强度下,测得的自旋结构因子达到123(8),表明反铁磁相的建立。此结果为探索 FHM 的低温相图提供了机会。相关成果以「Antiferromagnetic phase transition in a 3D fermionic Hubbard model」为题发表在Nature上,第一作者为Hou-Ji Shao, Yu-Xuan Wang为共同一作。

论文截图

潘建伟,1970年3月生于浙江东阳,实验物理学博士,中国科学技术大学教授,中国科学院院士,发展中国家科学院院士,奥地利科学院外籍院士,现任中科院量子信息与量子科技创新研究院院长。2001年,潘建伟在奥地利维也纳大学完成五年的博士后研究后,回到母校中国科学技术大学,成为近代物理系的教授,当时他年仅31岁。回国后,他带领团队专注于量子光学、量子信息和量子力学基础问题的研究,推动了中国量子信息技术的进程,成为国际上颇具影响力的科学家,被誉为「最接近诺贝尔奖的中国科学家」。
三维费米子哈伯德模型中的反铁磁相变
费米子哈伯德模型(FHM)描述了由强电子-电子相关性引起的广泛的物理现象,包括非常规超导的推测机制。然而,解决其低温物理问题在理论上或数值上都具有挑战性。光学晶格中的超冷费米子提供了一个干净且控制良好的平台,为模拟FHM提供了一条途径。在半填充状态下掺杂FHM模拟器的反铁磁基态有望产生各种奇异相,为研究高温超导性提供有价值的见解。虽然在短距离和长距离上已经观察到反铁磁相关,但反铁磁相还没有实现,因为它需要在一个大而均匀的量子模拟器中足够低的温度。
费米子哈伯德模型(FHM)的哈密顿量采用一种简单的形式,由两项组成:一项表示最近邻居的跳跃t,另一项表示具有相反自旋的电子之间的现场相互作用U。FHM可以描述广泛的强相关电子物理,包括相互作用驱动的金属到绝缘体的转变,量子磁性和非常规超导性。然而,尽管经过了60年的深入研究,对其低温物理特性的准确理解仍然未知。精确的解析解只能在一维或无限空间维度的极限中得到。尽管已经开发了各种先进的数值技术,但控制的定量研究仍然很少,特别是在低温状态下。量子蒙特卡罗(QMC)模拟通常会遇到负号问题,而其他方法,如密度矩阵重整化组,由于计算机内存需求随着系统大小呈指数增长而受到限制。即使在半填充的情况下,对于低温下足够大的系统,模拟在计算上也会变得令人望而却步。
在过去的二十年中,现代激光和原子技术的发展导致了在光学晶格中使用超冷原子的FHM的实验实现。对哈密顿参数的精确控制使这些超冷原子系统成为探索低温和掺杂状态下FHM强相关特性的强大平台,这些特性是通过分析和数值方法难以获得的。要实现这一目标,关键和不可避免的一步是在FHM中实现Néel相变和反铁磁相。这需要达到低温,制备大型均匀系统和开发新的探测技术。沿着这些思路,已经取得了许多重要进展。在三维空间中,莫特相和带绝缘相的实现,以及短程量子磁性的观察已被报道。值得注意的是,自旋结构因子(SSF)在比nsamel温度TN高约40%的温度下达到了Sπ≈2,表明存在短程反铁磁相关。
在这项工作中,研究人员开发了一个大型量子模拟器,通过结合两个关键进展来探索FHM的低温物理:在盒阱中产生低温均匀费米气体和展示具有均匀位势的三维(3D)平顶光学晶格。在半填充时,FHM的哈密顿量表现出SU(2)对称性,并且随着温度T的降低,它在TN处经历向反铁磁Néel相的转变,SU(2)对称性自发破坏。因此,该反铁磁相变与三维经典Heisenberg模型具有相同的普遍性,这意味着SSF应表现出发散性行为,其临界指数为γ≠(T−TN)−γ,且临界点指数为γ≃1.396。
实验方案和设置
为了研究3D费米哈伯德模型(FHM)中的量子磁性,作者结合盒式陷阱和平顶光学晶格的方法(图1),在中心区域直径49.5 μm内,确保最近邻跳跃t、现场相互作用U和化学势µ基本恒定。这种系统通过低温均质费米气体和近绝热晶格加载,有效实现低单粒子熵,进而制备具有极低3D费米子哈伯德系统单粒子熵的均匀费米气体。系统由6Li原子组成,分布在超精细能级|1⟩和|3⟩之间,且在568G磁场下被限制在圆柱形盒式阱内,达到密度约6.64×10¹²cm⁻³和0.041(1)TF的低温。在18ms内逐渐增加晶格深度并在12ms内调整磁场,实现不同现场相互作用U,最终生成t/h=1.40(1)kHz和U/h范围从6.04(2)kHz到28.83(9)kHz。图1b显示了U/t=11且半填充状态下的代表性原位图像,中心区域原子密度高度均匀。为研究系统内长程反铁磁序,使用了自旋敏感相干布拉格散射技术,图1d显示布拉格信号强度约为参考信号的100倍。

图 1|实验方案和设置
作者从半填充的费米哈伯德模型开始,研究其反铁磁相变(图2a)。在高温下,系统表现出金属行为(小U)或莫特绝缘态(大U),在TN以下和小U处,由自旋密度波(SDW)引起的尼尔跃迁,TN达到最大值时的最佳相互作用强度为Uopt。实验结果显示,在U ≈ 11.5t时,TN达到最大值,这是由于边界附近原子密度偏离半填充以及晶格势中残留无序性引起的。SSF的测量结果(图2b)显示,随着U的增加,Sπ从小值逐渐增加,在U ≈ 11.96t时达到最大,然后在U ≈ 20.62t时降至最低。作者发现,U/t ≤ 8和U/t ≥ 16的数据可以被Néel转变点捕捉,显示出系统在相互作用、温度和原子密度参数空间中接近临界点时的普遍性。

图 2|自旋结构因子 Sπ 作为 U/t 的函数
研究测量了Sπ作为每个粒子初始熵s的函数,并在图3a-d中显示了U/t≈11.75、8.21、18.06和5.31的结果。对于U≈11.75t和8.21t,幂律拟合显示临界熵分别为sc≈0.27kB和0.20kB(图3a、b)。相比之下,对于U≈18.06t,临界标度较弱,表明系统接近但未达到尼尔跃迁;对于U≈5.31t,临界缩放几乎不可辨别(图3c、d)。基于盒式阱和高温QMC数据的LDA计算,Sπ值与实验值吻合良好(U≈5.31t),但对于U≈8.21t,数值结果大于实验值,主要因非绝热性和晶格势中无序性。作者建议通过实验和数值比较确定温度。然而,由于误差较大和对s变化不敏感,使用图3中的s展示尼尔转变最为合适。考虑掺杂效应,理论预测掺杂10-20%时尼尔温度降低至零,且基态可能从反铁磁转变为不相称的SDW态,具体机制仍需进一步研究。

图 3:自旋结构因子 Sπ作为每个粒子 s 初始熵的函数
在实验中,作者在U ≈ 11.75t和半填充时,在最低温度下制备了费米子哈伯德系统。相图(图4a)显示纵轴表示费米子哈伯德系统每个粒子的熵sL,蓝点和粗箭头分别表示测量的s和估计的sL,作为每个晶格位点n的平均密度的函数,其中n = 1对应半填充。sL和s之间的差异表明熵的非绝热增加。Sπ的实验结果(图4b左)显示其在临界点附近急剧变化,实验数据在n < 0.91或n > 1.11时拟合良好,得到nc,s = 0.95(1)和nc,l = 1.07(1)的临界值。此外,双对数图(图4右)中,数据点折叠成斜率为-1.396的实线,表明与3D海森堡普适性一致,尽管实验数据不足以精确确定磁临界指数γ。

图 4|自旋结构因子 Sπ 作为每个位点平均密度 n 的函数
作者开发了一个先进的量子模拟平台,拥有约800,000个晶格位点,具有几乎均匀的哈伯德参数和远低于TN的温度,并观察到了SSF的关键分歧,为反铁磁相变提供了确凿证据。该装置为探索低温和掺杂的FHM25物理提供了机会,使作者能够通过调整层间耦合强度来研究3D或准2D中的奇异量子相,如更高维度的自旋电荷分离、排斥设置中的赝能隙和特定填充下的条纹顺序。这些研究可以通过自旋敏感布拉格光衍射、动量分辨微波光谱和长波长限制中的布拉格散射等技术实现。此外,通过在装置中添加光学超晶格,作者可以实现耦合平板阵列并探索可能的d波配对。这些量子模拟将提供有价值的实验数据,增强作者对量子磁性在高温超导机制中作用的理解。作者还计划通过调整原子相互作用以使其具有吸引力,在有吸引力的FHM中实现长期寻求的单带超流体,并在晶格背景下探索BCS-BEC交叉的基础物理现象。
该工作推进了对费米子哈伯德模型的理解,为进一步求解该模型、获取其低温相图奠定了基础,也首次展现了量子模拟在解决经典计算机无法胜任的重要科学问题上的巨大优势。相关成果以「Antiferromagnetic phase transition in a 3D fermionic Hubbard model」为题发表在Nature上,第一作者为Hou-Ji Shao, Yu-Xuan Wang为共同一作。
另外,2024年2月7日,中国科学技术大学潘建伟、姚星灿及陈宇翱共同通讯在Nature 在线发表题为「Observation and quantification of the pseudogap in unitary Fermi gases」的研究论文,该研究报告了通过动量分辨微波光谱精确测量费米子谱函数,在没有末态相互作用的虚假影响的情况下,在锂-6原子的均匀统一费米气体中观察到对波动驱动的赝隙。通过光谱分析,定量地确定了对间隙、逆对寿命和单粒子散射率的温度依赖性。该研究发现在超流体转变温度以上存在较大的赝隙。逆偶寿命表现为热激活指数行为,揭示了微观虚偶断裂和复合机制。得到的与温度无关的大单粒子散射率与普朗克极限所设定的散射率相当。总之,该研究的发现定量地描述了强相互作用费米气体中的赝隙,并支持了预形成对作为超流动性前兆的作用。(阅读原文:https://www.nature.com/articles/s41586-023-06964-y)
2024年5月2日,中国科学技术大学潘建伟及陆朝阳共同通讯在Science 在线发表题为「Realization of fractional quantum Hall state with interacting photons」的研究论文,该研究在二维电路量子电动力学系统上使用基于光子封锁和工程规范场的可编程片上平台演示了光子FQH态的晶格版本。(阅读原文:https://www.science.org/doi/10.1126/science.ado3912)
2024年5月15日,中国科学技术大学潘建伟及包小辉共同通讯在Nature 在线发表题为「Creation of memory–memory entanglement in a metropolitan quantum network」的研究论文,该研究报告了在城域上的多节点量子网络中创建内存-内存纠缠。(阅读原文:https://www.nature.com/articles/s41586-024-07308-0)
本篇论文链接:
https://www.nature.com/articles/s41586-024-07689-2
来源:高分子科学前沿,iNature,版权属于原作者,爱科会易仅用于学术交流